Indexed Priority Queue Package

Performance

We first analyze the cost of extracting the minimum time and inserting the new time. The new time for a reaction depends on its propensity. In the next reaction method, the time is increased by an exponential deviate whose mean is the inverse of the propensity. For this test, we simply advance the time by the inverse of the propensity to obtain the average behavior. We first consider the case of unit propensities. Then we consider sets of propensities which are geometric series whose first and last elements differ by 1/10, 1/100, and 1/1000. The execution times (in nanoseconds) are given below.

For unit propensities, the simple implementation of linear search is the fastest for up to 16 reactions. For larger problems, hashing yields the best performance. For small problems, the binary heap is no more than a factor of two slower that linear search. For 1024 reactions, the binary heap is 5 times slower than the hashing method. The partitioning methods (particularly the size adaptive and the cost adaptive variations) perform well. They are not as fast as hashing, but they out-perform the binary heap methods. Recall that the binary heap methods have computational complexity 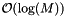compared to 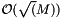for the partitioning methods, but even for up to 1024 reactions the former has better performance.

Switching to a geometric series for the propensites has little effect on the linear search methods and the partition methods. It makes the hashing methods a little slower because the hash table is rebuilt more often. The switch is a modest help to the binary heap methods. Fewer swaps are required when inserting the new times.

Unit propensities.

Geometric series with overall factor 1/10.

Geometric series with overall factor 1/100.

Geometric series with overall factor 1/1000.

Now we consider the cost of changing the time for an element. We first consider changing the time by a large amount. In particular, the time for the 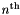reaction is changed to the time for the 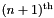reaction.

The computational complexities of this operation for linear search, partitioning, and hashing are each constant. The linear search method has the lowest execution time. The cost for the partitioning method is an order of magnitude greater than that for linear search. The cost for the hashing method is a factor of two greater than that for partioning. For the binary heap, the cost grows with increasing problem size. For small problems it is comparable to partitioning or hashing, but it is significantly more expensive for larger problems.

Switching to a geometric series for the propensities has little effect on the performance for any of the methods.

Unit propensities.

Geometric series with overall factor 1/10.

Geometric series with overall factor 1/100.

Geometric series with overall factor 1/1000.

Finally we consider the cost of changing the time by a small amount. Specifically, we increase or decrease the time by the inverse of the maximum propensity. Again, the computational complexities of this operation for linear search, partitioning, and hashing are each constant. For linear search and hashing, the costs for changing by a large amount and a small amount are the same. For partitioning, changing by a small amount is a little less expensive. For the binary heap, the expected complexity of changing an element by a small amount is constant. The element will only move by a small amount in the heap. The costs for the pointer implementation of the binary heap are a little faster than the best hashing method.

Unit propensities.

Geometric series with overall factor 1/10.

Geometric series with overall factor 1/100.

Geometric series with overall factor 1/1000.